Pengertian Gerbang Logika Dasar dan Jenis-jenisnya

Pengertian Gerbang Logika Dasar dan Jenis-jenisnya– Gerbang Logika atau dalam bahasa Inggris disebut dengan Logic Gate adalah dasar pembentuk Sistem Elektronika Digital yang berfungsi untuk mengubah satu atau beberapa Input (masukan) menjadi sebuah sinyal Output (Keluaran) Logis. Gerbang Logika beroperasi berdasarkan sistem bilangan biner yaitu bilangan yang hanya memiliki 2 kode simbol yakni 0 dan 1 dengan menggunakan Teori Aljabar Boolean.

Gerbang Logika yang diterapkan dalam Sistem Elektronika Digital pada dasarnya menggunakan Komponen-komponen Elektronika seperti Integrated Circuit (IC), Dioda, Transistor, Relay, Optik maupun Elemen Mekanikal.

Jenis-jenis Gerbang Logika Dasar dan Simbolnya

Terdapat 7 jenis Gerbang Logika Dasar yang membentuk sebuah Sistem Elektronika Digital, yaitu :

1. Gerbang AND
2. Gerbang OR
3. Gerbang NOT
4. Gerbang NAND
5. Gerbang NOR
6. Gerbang X-OR (Exclusive OR)
7. Gerbang X-NOR (Exlusive NOR)

Tabel yang berisikan kombinasi-kombinasi Variabel Input (Masukan) yang menghasilkan Output (Keluaran) Logis disebut dengan “Tabel Kebenaran” atau “Truth Table”.

Input dan Output pada Gerbang Logika hanya memiliki 2 level. Kedua Level tersebut pada umumnya dapat dilambangkan dengan :

• HIGH (tinggi) dan LOW (rendah)
• TRUE (benar) dan FALSE (salah)
• ON (Hidup) dan OFF (Mati)
• 1 dan 0

Contoh Penerapannya ke dalam Rangkaian Elektronika yang memakai Transistor TTL (Transistor-transistor Logic),  maka 0V dalam Rangkaian akan diasumsikan sebagai “LOW” atau “0” sedangkan 5V akan diasumsikan sebagai “HIGH” atau “1”.

Berikut ini adalah Penjelasan singkat mengenai 7 jenis Gerbang Logika Dasar beserta Simbol dan Tabel Kebenarannya.

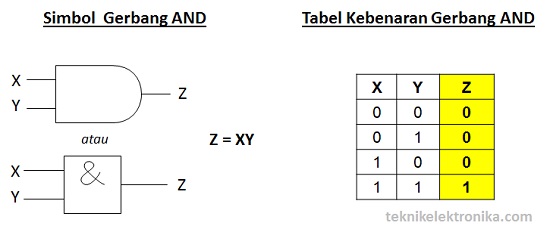
Gerbang AND (AND Gate)

Gerbang AND memerlukan 2 atau lebih Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang AND akan menghasilkan Keluaran (Output) Logika 1 jika semua masukan (Input) bernilai Logika 1 dan akan menghasilkan Keluaran (Output) Logika 0 jika salah satu dari masukan (Input) bernilai Logika 0. Simbol yang menandakan Operasi Gerbang Logika AND adalah tanda titik (“.”) atau tidak memakai tanda sama sekali. Contohnya : Z = X.Y atau Z = XY.

Simbol dan Tabel Kebenaran Gerbang AND (AND Gate)

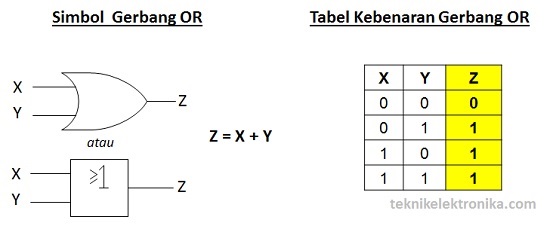
Gerbang OR (OR Gate)

Gerbang OR memerlukan 2 atau lebih Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang OR akan menghasilkan Keluaran (Output) 1 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin menghasilkan Keluaran (Output) Logika 0, maka semua Masukan (Input) harus bernilai Logika 0.

Simbol yang menandakan Operasi Logika OR adalah tanda Plus (“+”). Contohnya : Z = X + Y.

Simbol dan Tabel Kebenaran Gerbang OR (OR Gate)

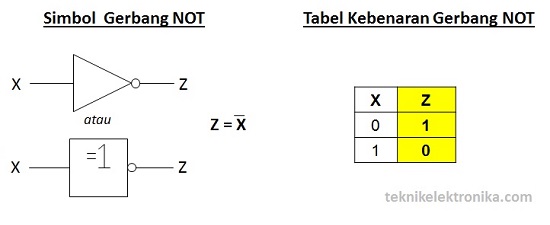
 Gerbang NOT (NOT Gate)

Gerbang NOT hanya memerlukan sebuah Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang NOT disebut juga dengan Inverter (Pembalik) karena menghasilkan Keluaran (Output) yang berlawanan (kebalikan) dengan Masukan atau Inputnya. Berarti jika kita ingin mendapatkan Keluaran (Output) dengan nilai Logika 0 maka Input atau Masukannya harus bernilai Logika 1. Gerbang NOT biasanya dilambangkan dengan simbol minus (“-“) di atas Variabel Inputnya.

Simbol dan Tabel Kebenaran Gerbang NOT (NOT Gate)  

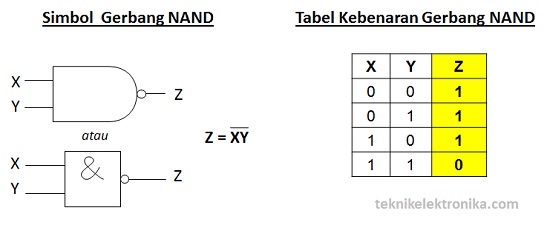
Gerbang NAND (NAND Gate)

Arti NAND adalah NOT AND atau BUKAN AND, Gerbang NAND merupakan kombinasi dari Gerbang AND dan Gerbang NOT yang menghasilkan kebalikan dari Keluaran (Output) Gerbang AND. Gerbang NAND akan menghasilkan Keluaran Logika 0 apabila semua Masukan (Input) pada Logika 1 dan jika terdapat sebuah Input yang bernilai Logika 0 maka akan menghasilkan Keluaran (Output) Logika 1.

Simbol dan Tabel Kebenaran Gerbang NAND (NAND Gate) 

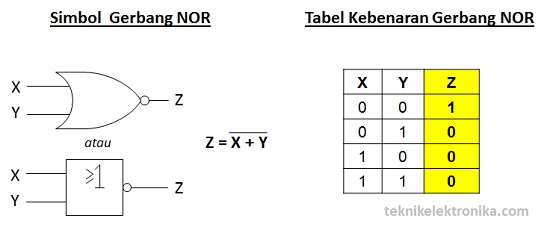
Gerbang NOR (NOR Gate)

Arti NOR adalah NOT OR atau BUKAN OR, Gerbang NOR merupakan kombinasi dari Gerbang OR dan Gerbang NOT yang menghasilkan kebalikan dari Keluaran (Output) Gerbang OR. Gerbang NOR akan menghasilkan Keluaran Logika 0 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin mendapatkan Keluaran Logika 1, maka semua Masukan (Input) harus bernilai Logika 0.

Simbol dan Tabel Kebenaran Gerbang NOR (NOR Gate) 

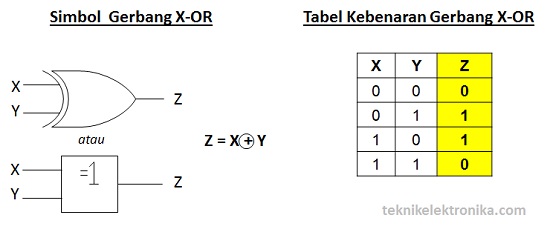
Gerbang X-OR (X-OR Gate)

X-OR adalah singkatan dari Exclusive OR yang terdiri dari 2 Masukan (Input) dan 1 Keluaran (Output) Logika. Gerbang X-OR akan menghasilkan Keluaran (Output) Logika 1 jika semua Masukan-masukannya (Input) mempunyai nilai Logika yang berbeda. Jika nilai Logika Inputnya sama, maka akan memberikan hasil Keluaran Logika 0.

Simbol dan Tabel Kebenaran Gerbang X-OR (X-OR Gate) 

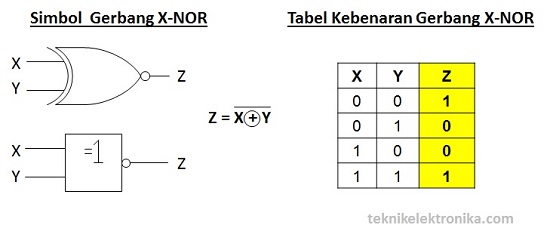
 Gerbang X-NOR (X-NOR Gate)

Seperti Gerbang X-OR,  Gerban X-NOR juga terdiri dari 2 Masukan (Input) dan 1 Keluaran (Output). X-NOR adalah singkatan dari Exclusive NOR dan merupakan kombinasi dari Gerbang X-OR dan Gerbang NOT. Gerbang X-NOR akan menghasilkan Keluaran (Output) Logika 1 jika semua Masukan atau Inputnya bernilai Logika yang sama dan akan menghasilkan Keluaran (Output) Logika 0 jika semua Masukan atau Inputnya bernilai Logika yang berbeda. Hal ini merupakan kebalikan dari Gerbang X-OR (Exclusive OR).

Simbol dan Tabel Kebenaran Gerbang X-NOR (X-NOR Gate) 

1. Bilangan Biner
Berbasis : 2
 
Lambang Bilangannya : 0, 1


Cara penulisannya : (1010)2
Dalam bahasa rakitan ditulis : 1010B 

2. Bilangan Octal

Berbasis : 8

Lambang Bilangannya : 0, 1, 2, 3, 4, 5, 6, 7

Cara penulisannya : (167)8

Dalam bahasa rakitan ditulis :167O 

3. Bilangan Hexa-Decimal

Berbasis : 16

Lambang Bilangannya : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Cara penulisannya : (9A7)16

Dalam bahasa rakitan ditulis : 9A7H 

4.Bilangan Decimal

Berbasis : 10

Lambang Bilangannya : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Cara penulisannya : (197)10

Dalam bahasa rakitan ditulis : 197D atau 197 

Contoh Soal Konversi

1. Konversi Desimal → Biner.

Gunakan pembagian dengan 2 secara suksesif sampai sisanya = 0. Sisa-sisa pembagian membentuk jawaban,

yaitu sisa yang pertama akan menjadi Least Significant Bit (LSB) dan sisa yang terakhir menjadi Most

Significant Bit (MSB). Atau menggunakan Ms. Excel dengan rumus =DEC2BIN(SEL)

Penyelesaian

1.Kita bagi 67 dengan 2, didapat bilangan bulat hasil bagi adalah 33 dengan hasil bagi adalah 1, atau

dengan kata lain 67 = 2 x 33 + 1

2.Selanjutnya bilangan bulat hasil bagi tersebut (33) kita bagi dengan 2 lagi, 33/2 = 16, sisa hasil bagi 1.

3.Kemudian kita ulangi lagi, 16/2 = 8, sisa hasil bagi 0.

4.Ulangi lagi langkah tersebut sampai bilangan bulat hasil bagi sama dengan 0. Setelah itu tulis sisa hasil

bagi mulai dari bawah ke atas.

5.Dengan demikian kita akan mendapatkan bahwa 6710 = 100001112.

67 / 2 = 33  sisa 1 (LSB)

  / 2  = 16  sisa 1

  / 2 = 8  sisa 0

  / 2 = 4  sisa 0

  / 2 = 2  sisa 0

  / 2 = 1  sisa 0

  / 2 = 0  sisa 1 (MSB) 

2. Konversi Desimal → Oktal.

Dengan rumus yang sama seperti Biner kita bisa lakukan juga untuk bilangan berbasis 8 (Oktal). Atau

menggunakan Ms. Excel dengan rumus =DEC2OCT(SEL)

Contoh:  6710 = …8

1.Pertama-tama 67/8 = 8, sisa 3

2.Lalu 8/8 = 1, sisa 0

3.Terakhir 1/8 = 0, sisa 1

4.Dengan demikian dari hasil perhitungan didapatkan 6710 = 1038

67 / 8 = 8  sisa 3

  /8 = 1  sisa 0

  /8 = 0  sisa 1

3. Konversi Desimal → Heksadesimal.

Dengan rumus yang sama seperti Biner & Oktal kita bisa lakukan juga untuk bilangan berbasis 16

(Heksadesimal). Atau menggunakan Ms. Excel dengan rumus =DEC2HEX(SEL)

Contoh:  6710 = …16

             9210 = …16

1.Pertama-tama 67/16 = 4, sisa 3

2.Lalu 4/16 = 0, sisa 4

3.Dengan demikian dari hasil perhitungan didapatkan 6710 = 4316

Pembahasan

1.Pertama-tama 92/16 = 5, sisa 12 ditulis C

2.Lalu 5/16 = 0, sisa 5

3.Dengan demikian dari hasil perhitungan didapatkan 9210 = 5C16

4. Konversi Biner → Desimal.

Untuk mengkonversikan Biner ke Desimal maka tinggal mengalikan setiap digit dari

bilangan tersebut dengan pangkat 0, 1, 2, … dst, dari basis mulai paling kanan. Atau

menggunakan Ms. Excel dengan rumus =BIN2DEC(SEL)

Contoh:  101102 = …10

Pembahasan

101102 =  0 x 2^0  = 0

  1 x 2^1   = 2

  1 x 2^2  = 4

  0 x 2^3   = 0

  1 x 2^4   = 16

  = 2210

5. Biner → Oktal

Untuk melakukan konversi biner ke octal lakukan bagi setiap 3 digit menjadi sebuah angaka

octal dimulai dari paling kanan. Atau menggunakan Ms. Excel dengan rumus

=BIN2OCT(SEL)

Contoh : 101102 = …8

Pembahasan

1. Pertama bagi menjadi kelompok yang terdiri dari 3 digit biner: 10 dan 110.

2. Kemudian konversi setiap kelompok dengan menggunakan perhitungan konversi biner ke

decimal

3. Sehingga didapat 101102 = 268

6. Konversi Biner → Heksadesimal.

-

Mirip dengan biner ke octal, hanya saja pembagian kelompok terdiri dari 4 digit biner. Selain

itu untuk nilai 10, 11, 12, …, 15 diganti dengan huruf A, B, C, …, F. Atau menggunakan

Ms. Excel dengan rumus =BIN2HEX(SEL)

Contoh : 1110102 = …16

Pembahasan

1.Bagi menjadi kelompok yang terdiri dari 4 digit biner: 11 dan 1010.

2.Kemudian konversi setiap kelompok dengan menggunakan perhitungan biner ke

decimal.

3.Sehingga didapat 1110102 = 3A16

7. Konversi Oktal → Desimal.

Anda perlu mengalikan digit dengan pangkat dari bilangan 8. Atau menggunakan Ms. Excel

dengan rumus =OCT2DEC(SEL)

Contoh : 3658 = …10

Pembahasan

3658  = (3 x 8^2)10 + (6 x 8^1)10 + (5 x 8^0)10

  = 192 + 48 + 5

  = 245

8. Konversi Oktal → Biner

Cara ini merupakan kebalikan cara konversi biner ke octal. Setiap digit oktal akan langsung

dikonversi ke biner lalu hasilnya digabungkan. Atau dengan Ms.Excel dengan rumus

=OCT2BIN(SEL)

Contoh : 548 = …2

Pembahasan

1.Hitung 58 = 1012 (Lihat decimal ke biner)

2.Lalu 48 = 1002

3.Sehingga 548 = 1011002

9. Konversi Oktal → Heksadesimal.

Ada 3 cara :  

- Konversi dahulu octal ke decimal lalu ke heksadesimal.

- Konversi dahulu octal ke biner lalu ke heksadesimal.

- =OCT2HEX(SEL)

Contoh : 3658 = …16

Pembahasan

1.Konversi octal ke biner → 3658 = 11 110 1012

2.   Konversi biner ke hexa → 11 110 1012 = F516

9. Konversi Heksadesimal → Desimal

Dengan mengalikan digit bilangan hexa dengan pangkat bilangan 16 dari kanan ke kiri mulai

dengan pangkat 0, 1, 2, …, dst. Atau dengan Ms. Excel dengan rumus =HEX2DEC(SEL)

Contoh : F516 = …8

Pembahasan

F516  = (15 x 16^1)10 + (5 x 16^0)10

  = 240 + 5

  = 245

10.Konversi Heksadesimal → Biner

Kebalikan dari biner → heksadesimal. Setiap digit hexa langsung dikonversi ke biner lalu

hasilnya dipadukan. Dengan rumus =HEX2BIN(SEL)

Contoh : F516 = …2

Pembahasan

1.F16 = 11112 (F16 → 1510 = 11112)

2.516 = 01012 (Harus dalam 4 digit biner)

3.F516 = 111101012

11. Konversi Heksadesimal → Oktal

Mirip dengan octal ke decimal. Konversi hexa ke biner dulu lalu dari biner ke octal. Dengan

rumus =HEX2OCT(SEL)

Contoh : F516 = …8

Pembahasan

1.F516  = 111101012

2.11 110 1012  = 3658

Sekian Sedikit penjelasan dari saya, Saya mohon maaf apabila ada

penjelasan yang kurang jelas terima kasih telah membaca.

Wassalamualaikum Wr. Wb.